L’altro giorno sono andato (… cosa volete è obbligatorio per i neo-iscritti) al corso di deontologia professionale dell’ordine degli ingegneri di Ravenna. Poiché tra un discorso interessante e l’altro c’erano anche discorsi un po’ noiosi mi è venuta la voglia di fare qualche dimostrazione matematica dei vecchi studi… e visto che ultimamente l’ho usato spesso, proprio la dimostrazione di cos (α-β).
Poi metterò anche le pagine del mio blocco appunti così vedete che è vero che gli ingegneri sono un po’ matti 🙂
La dimostrazione di cos(α-β) è la base per la facile dimostrazione delle formule gemelle
cos (α-β)
sin (α-β)
sin (α+β)
cos (α-β) = ?

Il segmento AB sulla circonferenza con c’entro nell’origine lo trasliamo di un angolo β in modo che il punto B vada a coincidere sull’asse x.
Deve ovviamente essere: 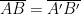

Per il famoso Pitagora
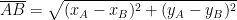
Ed anche

E imponiamo l’uguaglianza dei segmenti:
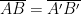
Poiché abbiamo tutte componenti positive possiamo elevare al quadrato e avere:

Quindi

Sempre dalla trigonometria risulta che:
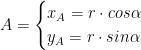
e

e
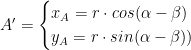
e
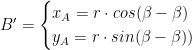
Quindi

e
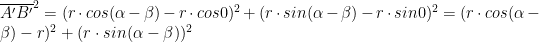
Imponiamo di avere un raggio pari ad 1: 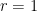
Abbiamo:

e

Poiché equivale l’uguaglianza: 
Abbiamo

e

Quindi se 
si ha:

→

→

→
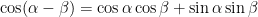
CVD.
Lo so… gli ingegneri tendono alla follia a volte… 😀



Mi piace:
Mi piace Caricamento...
.
nell’origine del punto
, una rotazione rispetto all’origine
di
e successivamente una nuova traslazione
che riporti A al suo posto 🙂
è
è:










