Rotazione rispetto ad un punto generico Ω(x0,y0)

Agosto 15, 2015Aprile 8, 2019 Fabio Bombardi

Adesso che nell’articolo sulle Coordinate Omogenee abbiamo imparato a comporre le trasformazioni nel piano possiamo facilmente ricavarci la formula di un punto ruotato rispetto ad un punto generico $\Omega(x_0,y_0)$ .

Per ottenerla basta applicare una operazione di traslazione $T_1$ nell’origine del punto $A$ , una rotazione rispetto all’origine $R$ di $A$ e successivamente una nuova traslazione $T_2$ che riporti A al suo posto 🙂

Quindi: $A^\prime = T_2\cdot R\cdot T_1\cdot A = \begin{bmatrix} 1 & 0 & x_0 \\ 0 & 1 & y_0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} \cos\beta & -\sin\beta & 0 \\ \sin\beta & \cos\beta & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & -x_0 \\ 0 & 1 & -y_0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

Ovvero:

$A^\prime = T_2\cdot R\cdot T_1\cdot A = \begin{bmatrix} \cos\beta & -\sin\beta & x_0 \\ \sin\beta & \cos\beta & y_0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & -x_0 \\ 0 & 1 & -y_0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

Ovvero:

$A^\prime = T_2\cdot R\cdot T_1\cdot A = \begin{bmatrix} \cos\beta & -\sin\beta & -x_0\cos\beta+y_0\sin\beta+x_0 \\ \sin\beta & \cos\beta & -x_0\sin\beta-y_0\cos\beta+y_0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

Quindi la matrice di rotazione rispetto a $\Omega(x_0,y_0)$ è

$R = \begin{bmatrix} \cos\beta & -\sin\beta & -x_0\cos\beta+y_0\sin\beta+x_0 \\ \sin\beta & \cos\beta & -x_0\sin\beta-y_0\cos\beta+y_0 \\ 0 & 0 & 1 \end{bmatrix}$

E il punto $A^\prime$ è:

$A^\prime = \begin{bmatrix} x\cdot\cos\beta-y\cdot\sin\beta-x_0\cos\beta+y_0\sin\beta+x_0 \\ x\cdot\sin\beta+y\cdot\cos\beta-x_0\sin\beta-y_0\cos\beta+y_0 \\ 1 \end{bmatrix} = \begin{bmatrix} (x-x_0)\cdot\cos\beta - (y-y_0)\cdot\sin\beta + x_0 \\ (x-x_0)\cdot\sin\beta+(y-y_0)\cdot\cos\beta+y_0 \\ 1 \end{bmatrix}$

$A^\prime = \begin{bmatrix} (x-x_0)\cdot\cos\beta - (y-y_0)\cdot\sin\beta + x_0 \\ (x-x_0)\cdot\sin\beta+(y-y_0)\cdot\cos\beta+y_0 \\ 1 \end{bmatrix}$

Coordinate omogenee

Agosto 7, 2015Aprile 8, 2019 Fabio Bombardi

Non possiamo con la rappresentazione matriciale presentata nell’articolo sulle Trasformazioni Nel Piano concatenare la rotazione e la scala con la traslazione. Questo perché in questo secondo caso abbiamo una somma matriciale e nei primi due abbiamo una moltiplicazione.
Possiamo però riscrivere le matrici nel cosiddetto “sistema di riferimento omogeneo”. Non starò qui a spiegare il concetto di sistema di riferimento omogeneo, dirò solo che un punto A la cui rappresentazione matriciale è $\begin{bmatrix} x \\ y \end{bmatrix}$ nel sistema di riferimento omogeneo diventa $\begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$
Le rispettive matrici di trasformazione diventano:

Traslazione: $T = \begin{bmatrix} 1 & 0 & \Delta x \\ 0 & 1 & \Delta y \\ 0 & 0 & 1 \end{bmatrix}$

Rotazione: $R = \begin{bmatrix} \cos\beta & -\sin\beta & 0 \\ \sin\beta & \cos\beta & 0 \\ 0 & 0 & 1 \end{bmatrix}$

Scala: $S = \begin{bmatrix} sx & 0 & 0 \\ 0 & sy & 0 \\ 0 & 0 & 1 \end{bmatrix}$

Vediamo se i conti ci tornano 🙂
Questa volta possiamo utilizzare la moltiplicazione tra matrici anche per la Traslazione.

Traslazione

$A^\prime = T \cdot A = \begin{bmatrix} 1 & 0 & \Delta x \\ 0 & 1 & \Delta y \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} x + \Delta x \\ y + \Delta y \\ 1 \end{bmatrix}$

Che è esattamente il nostro punto traslato in coordinate omogenee.

Rotazione

$A^\prime = T \cdot A = \begin{bmatrix} \cos\beta & -\sin\beta & 0 \\ \sin\beta & \cos\beta & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} x\cdot\cos\beta - y\cdot\sin\beta \\ x\cdot\sin\beta + y\cdot\cos\beta \\ 1 \end{bmatrix}$

Che è esattamente il nostro punto ruotato in coordinate omogenee.

Scala

$A^\prime = T \cdot A = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} x\cdot s_x \\ y\cdot s_y \\ 1 \end{bmatrix}$

Che è esattamente il nostro punto scalato in coordinate omogenee.

Regola di composizione

Quando si compongono 2 o più trasformazioni la precedente è sempre a destra della successiva. Ovvero se abbiamo 3 trasformazioni $\Theta_1$ , $\Theta_2$ , $\Theta_3$ che vengono fatte in sequenza: Prima $\Theta_1$ , poi $\Theta_2$ e per ultima $\Theta_3$ il punto A’ sarà dato da:

$A^\prime = \Theta_3\cdot\Theta_2\cdot\Theta_1\cdot A$

Trasformazioni nel piano

Luglio 30, 2015Aprile 8, 2019 Fabio Bombardi

Visto che abbiamo appena parlato del cos(α-β) in un nostro precedente articolo (http://www.versionestabile.it/blog/cos-alpha-beta-ve-lo-ricordate) perché non parlare delle trasfromazioni nel piano, per arrivare ad ottenere la formula della rotazione di un punto rispetto ad un punto generico Ω(x0,y0)? 🙂

Traslazione

traslazione_a_aprimo

Un punto A viene traslato in A’ di Δx e Δy

Quindi: $A^\prime = \begin{bmatrix} x \\ y \end{bmatrix}$

Mentre A’ sarà: $A^\prime = \begin{bmatrix} x^\prime \\ y^\prime \end{bmatrix} = \begin{bmatrix} x + \Delta x \\ y + \Delta y \end{bmatrix}$

In rappresentazione matriciale potremmo scrivere

$A^\prime = T + A = \begin{bmatrix} \Delta x \\ \Delta y \end{bmatrix} + \begin{bmatrix} x \\ y \end{bmatrix}$

Rotazione rispetto all’origine

rotazione rispetto origine

Qui abbiamo: $A = \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x = r\cdot\cos\alpha \\ y = r\cdot\sin\alpha \end{bmatrix}$

Il suo punto A’ ruotato di β in senso antiorario sarà: $A^\prime = \begin{bmatrix} x^\prime \\ y^\prime \end{bmatrix} = \begin{bmatrix} x^\prime = r\cdot\cos(\alpha + \beta) \\ y^\prime = r\cdot\sin(\alpha + \beta) \end{bmatrix}$

Ecco che ci vengono in aiuto le tanto dimostrate formule del coseno e del seno della somma di angoli! 😀

$A^\prime = \begin{bmatrix} x^\prime \\ y^\prime \end{bmatrix} = \begin{bmatrix} x^\prime = r\cdot\cos(\alpha + \beta) \\ y^\prime = r\cdot\sin(\alpha + \beta) \end{bmatrix} = \begin{bmatrix} x^\prime = r\cdot\cos\alpha\cos\beta - r\cdot\sin\alpha\sin\beta \\ y^\prime = r\cdot\sin\alpha\cos\beta) + r\cdot\cos\alpha\sin\beta \end{bmatrix}$

Poichè

$\begin{cases} x = r\cdot\cos\alpha \\ y = r\cdot\sin\alpha \end{cases}$

A’ diventa:

In rappresentazione matriciale diventa $latex

$A^\prime = R \cdot A = \begin{bmatrix} \cos\beta & -\sin\beta \\ \sin\beta & \cos\beta \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix}$

Scala

Nell’immagine precedente si è ipotizzato: $\begin{cases} scala x = s_x = \frac{1}{2} \\ scala y = s_y = \frac{1}{2} \end{cases}$

Qui abbiamo: $A = \begin{bmatrix} x \\ y \end{bmatrix}$

Il suo punto A’ scalato di sx e sy lo scriviamo come: $A^\prime = \begin{bmatrix} x^\prime \\ y^\prime \end{bmatrix} = \begin{bmatrix} x^\prime = x\cdot s_x \\ y^\prime = y\cdot s_y \end{bmatrix}$

In rappresentazione matriciale diventa $latex

$A^\prime = S \cdot A = \begin{bmatrix} s_x \\ s_y \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix}$

Formule trigonometriche della somma e differenza di due angoli

Luglio 14, 2015Aprile 8, 2019 Fabio Bombardi

Con l’arrivo dell’Estate, ls scuole chiudono e io penso sempre a quanto era bello poter contare in 3 mesi di vacanze! 😀

E quanto ritorna la nostalgia mi viene da scrivere un po’ di formule matematiche.

Visto che avevo iniziato con la trigonometria… continuiamo con la trigonometria!

Dalla formula del coseno della differenza di due angoli otteniamo facilmene le formule per

– $\cos(\alpha+\beta)$
– $\sin(\alpha-\beta)$
– $\sin(\alpha+\beta)$

Dalle immagine sopra vediamo che:

– $\cos(\alpha) = \sin(\frac{\pi}{2}-\alpha)$
– $\sin(\alpha) = \cos(\frac{\pi}{2}-\alpha)$
– $\sin(-\alpha) = -\sin\alpha$
– $\cos(-\alpha) = \cos(\alpha)$

$\cos(\alpha+\beta) = \cos\alpha\cos\beta - \sin\alpha\sin\beta$

infatti

$\cos(\alpha+\beta) = \cos(\alpha-(-\beta)) = \cos\alpha\cos(-\beta) + \sin\alpha\sin(-\beta) = \cos\alpha\cos\beta - \sin\alpha\sin\beta$

$\sin(\alpha+\beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta$

infatti

$\sin(\alpha+\beta) = \cos(\frac{\pi}{2}-(\alpha+\beta)) = \cos((\frac{\pi}{2}-\alpha)-\beta)) = \cos(\frac{\pi}{2}-\alpha)\cos\beta + \sin(\frac{\pi}{2}-\alpha)\sin\beta = \sin\alpha\cos\beta + \cos\alpha\sin\beta$

$\sin(\alpha-\beta) = \sin\alpha\cos\beta - \cos\alpha\sin\beta$

infatti

$\sin(\alpha-\beta) = \cos(\frac{\pi}{2}-(\alpha-\beta)) = \cos((\frac{\pi}{2}-\alpha)+\beta)) = \cos(\frac{\pi}{2}-\alpha)\cos\beta - \sin(\frac{\pi}{2}-\alpha)\sin\beta) = \sin\alpha\cos\beta - \cos\alpha\sin\beta$

cos (α – β) ve lo ricordate?

Luglio 4, 2015Aprile 8, 2019 Fabio Bombardi

L’altro giorno sono andato (… cosa volete è obbligatorio per i neo-iscritti) al corso di deontologia professionale dell’ordine degli ingegneri di Ravenna. Poiché tra un discorso interessante e l’altro c’erano anche discorsi un po’ noiosi mi è venuta la voglia di fare qualche dimostrazione matematica dei vecchi studi… e visto che ultimamente l’ho usato spesso, proprio la dimostrazione di cos (α-β).

Poi metterò anche le pagine del mio blocco appunti così vedete che è vero che gli ingegneri sono un po’ matti 🙂

La dimostrazione di cos(α-β) è la base per la facile dimostrazione delle formule gemelle

cos (α-β)
sin (α-β)
sin (α+β)

cos (α-β) = ?

Il segmento AB sulla circonferenza con c’entro nell’origine lo trasliamo di un angolo β in modo che il punto B vada a coincidere sull’asse x.

Deve ovviamente essere: $\overline{AB}=\overline{A'B'}$

Per il famoso Pitagora

$\overline{AB} = \sqrt{(x_A-x_B)^2+(y_A-y_B)^2}$

Ed anche

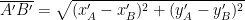
$\overline{A^\prime B^\prime} = \sqrt{(x_A^\prime-x_B^\prime)^2+(y_A^\prime-y_B^\prime)^2}$

E imponiamo l’uguaglianza dei segmenti:

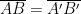
$\overline{AB} = \overline{A^\prime B^\prime}$

Poiché abbiamo tutte componenti positive possiamo elevare al quadrato e avere:

$\overline{AB}^2 = \overline{A^\prime B^\prime}^2$

Quindi

$(x_A-x_B)^2+(y_A-y_B)^2 = (x_A^\prime-x_B^\prime)^2+(y_A^\prime-y_B^\prime)^2$

Sempre dalla trigonometria risulta che:

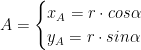
$A = \begin{cases} x_A=r \cdot cos\alpha \\ y_A = r \cdot sin\alpha \end{cases}$

$B = \begin{cases} x_A=r \cdot cos\beta \\ y_A = r \cdot sin\beta \end{cases}$

$A^\prime = \begin{cases} x_A=r \cdot cos(\alpha-\beta) \\ y_A = r \cdot sin(\alpha-\beta)) \end{cases}$

$B^\prime = \begin{cases} x_A=r \cdot cos(\beta-\beta) \\ y_A = r \cdot sin(\beta-\beta)) \end{cases}$

Quindi

$\overline{AB}^2 = (r\cdot cos\alpha - r\cdot cos\beta)^2+(r\cdot sin\alpha-r\cdot sin\beta)^2$

$\overline{A^\prime B^\prime}^2 = (r\cdot cos(\alpha-\beta) - r\cdot cos0)^2+(r\cdot sin(\alpha-\beta) - r\cdot sin0)^2 = (r\cdot cos(\alpha-\beta) - r)^2+(r\cdot sin(\alpha-\beta))^2$

Imponiamo di avere un raggio pari ad 1: 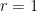$r=1$

Abbiamo:

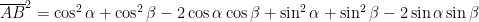
$\overline{AB}^2 = \cos^2\alpha + \cos^2\beta - 2\cos\alpha\cos\beta + \sin^2\alpha + \sin^2\beta-2\sin\alpha\sin\beta$

$\overline{A^\prime B^\prime}^2 = \cos^2(\alpha-\beta) + 1 - 2\cos(\alpha-\beta) + \sin^2(\alpha-\beta)$

Poiché equivale l’uguaglianza: $\cos^2\theta + \sin^2\theta = 1$

Abbiamo

$\overline{AB}^2 = (\cos^2\alpha + \sin^2\alpha) + (\cos^2\beta + \sin^2\beta) - 2\cos\alpha\cos\beta -2\sin\alpha\sin\beta = 1 + 1 - 2\cos\alpha\cos\beta -2\sin\alpha\sin\beta = 2 - 2\cos\alpha\cos\beta -2\sin\alpha\sin\beta$

$\overline{A^\prime B^\prime}^2 = (\cos^2(\alpha-\beta) + \sin^2(\alpha-\beta))+ 1 - 2\cos(\alpha-\beta) = 1 + 1 - 2\cos(\alpha-\beta) = 2 - 2\cos(\alpha-\beta)$

Quindi se $\overline{AB}^2 = \overline{A^\prime B^\prime}^2$

si ha:
$2 - 2\cos\alpha\cos\beta - 2\sin\alpha\sin\beta = 2 - 2\cos(\alpha-\beta)$

→

$(2 - 2) - 2\cos\alpha\cos\beta - 2\sin\alpha\sin\beta = - \cos(\alpha-\beta)$

→

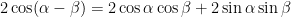
$2\cos(\alpha-\beta) = 2\cos\alpha\cos\beta + 2\sin\alpha\sin\beta$

→

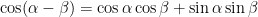
$\cos(\alpha-\beta) = \cos\alpha\cos\beta + \sin\alpha\sin\beta$

CVD.

Lo so… gli ingegneri tendono alla follia a volte… 😀

versionestabile

blog

Geometria

Rotazione rispetto ad un punto generico Ω(x0,y0)

Mi piace: